決定木の予測値が天井や底に張り付いてしまう

決定木の予測値が天井や底に張り付いてしまう。
RandomForestやXGBoost、LightGBMなどの決定木ベースの予測モデルで数値予測をしたところ同じ値が出続けてしまう。
なぜこのような事が起こるか。現象を確認しながら原因を解説する。

現象

決定木の予測値が天井や底に張り付いてしまう現象は再現ができる。

決定木で予測値が張り付く現象を再現

まずは右肩上がりに増えるデータとして y=0.5x のデータを用意する。

import matplotlib.pyplot as plt
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestRegressor

# dataset
x = np.linspace(0, 10, 100)
y = x * 0.5

# Set data on graph
plt.plot(x, y, label="y=0.5x")
# Set legend
plt.legend()
# Show graph
plt.show()

正常にデータができると以下のような線形のデータができる。

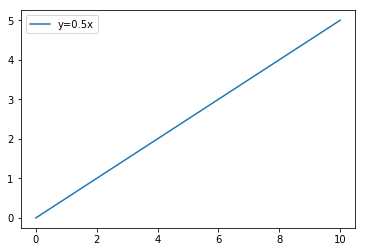
線形データ

このデータを前半70％を学習データ、残りをテストデータに分ける。

# split data
train_rate = 0.7
train_size = int(len(x) * train_rate)
x_train, x_test, y_train, y_test = x[0:train_size], x[train_size:len(x)], y[0:train_size], y[train_size:len(y)]

# Show graph
plt.plot(x_train, y_train, label="y=0.5x(train)")
plt.plot(x_test, y_test, label="y=0.5x(test)")
plt.legend()
plt.show()

すると以下のように線形データが学習用とテスト用に分かれる。

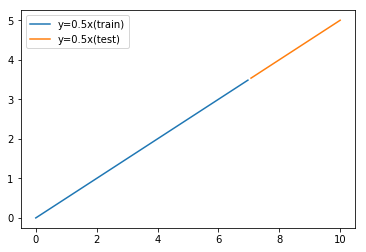
線形データ（学習とテスト）

そして学習用のデータを決定木で学習させて、テストデータを使って予測結果を確認する。
今回は決定木モデルとして RandomForest を使う。

# Train and Predict
reg = RandomForestRegressor(random_state=0)
reg = reg.fit(np.array(x_train).reshape(-1,1), y_train)
y_pred = reg.predict(np.array(x_test).reshape(-1,1))

# Show graph
plt.plot(x_train, y_train, label="y=0.5x(train)")
plt.plot(x_test, y_test, label="y=0.5x(test)")
plt.plot(x_test, y_pred, label="y_pred")
plt.legend()
plt.show()

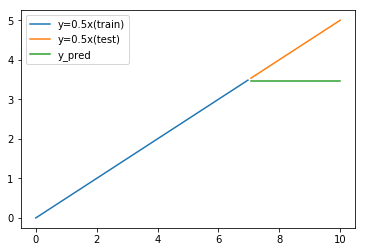
すると以下のような結果となる。
予測結果が天井に張り付いてしまい、実際のテストデータと異なる結果になっていることがわかる。

RandomForestの予測結果

線形回帰と比較

線形回帰モデルで予測すればこのような予測結果の固定化は起こらない。

# Train and Predict
from sklearn.linear_model import LinearRegression
reg = LinearRegression()
reg = reg.fit(np.array(x_train).reshape(-1,1), y_train)
y_pred = reg.predict(np.array(x_test).reshape(-1,1))

# Show graph
plt.plot(x_train, y_train, label="y=0.5x(train)")
plt.plot(x_test, y_test, label="y=0.5x(test)")
plt.plot(x_test, y_pred, label="y_pred")
plt.legend()
plt.show()

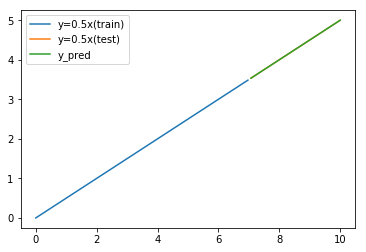
線形回帰の予測結果

予測結果が固定値になってしまう原因

予測結果が固定値になってしまう原因は決定木の仕組みにある。

決定木とは以下の仕組みを言う。
RandomForestやXGBoostも木の形を変えたり、複数の木を作って組み合わせたりするが、基本の仕組みは同じだ。

値をチェックして値の大小で分岐する
分岐した先の値を予測値として採用する
分岐に用いる閾値と分岐先の値を学習データに合うように決める

ここで重要なのは、「分岐先の値を学習データで決まる」ということ。
決定木の末端である予測値を実とするならば、枝の先の実の大きさは学習した時点で確定する。
つまり入力値である説明変数をどれだけ大きくしようと、決定木では常に学習データの最大値と同じルートを通り、常に同じ実（＝予測値）を得ることになる。

先の y=0.5x のデータで言えば、学習データで予測値の最大値は x=7 の場合で 3.5 と決まっており、学習によって作成された決定木から得られる予測結果の最大値は 3.5 となっているわけである。

つまりテストデータや現実でのデータの範囲が、学習データの範囲に収まらない場合に決定木を使うと予測値が学習データの限界で止まってしまう。

対処法

では決定木は使えないかというとそうではない。

予測対象である目的変数の変化する範囲を限定できないのであれば、変化の範囲がある程度決まっている値を目的変数とすれば良い。

差分値を目的変数にする

仮にxが等間隔の離散値だとして、t-1番目とt番目のyの差分を目的変数とすると、 y=0.5x の例ではxに対して一定の差分値が得られる。

import pandas as pd
df_data = pd.DataFrame()
df_data["x"] = x
df_data["y"] = y
df_data["y_diff"] = df_data["y"] - df_data["y"].shift(1)
df_data = df_data.dropna()

# split data
df_train, df_test = df_data.iloc[0:train_size], df_data.iloc[train_size:] 

# Show graph
plt.plot(df_train["x"], df_train["y_diff"], label="y=0.5x(train) diff")
plt.plot(df_test["x"], df_test["y_diff"], label="y=0.5x(test) diff")
plt.legend()
plt.show()

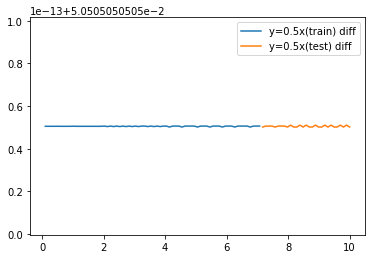
線形データの差分

この差分値は学習データでもテストデータでも変動範囲は同じなので、目的変数として差分値を学習させる。
そしてテストデータから得られた差分の予測値を元のyに加えてyの予測値として復元すると、先程は予測できなかった 3.5 以上の値も予測できることがわかる。

# Train and Predict difference
reg = RandomForestRegressor(random_state=0)
reg = reg.fit(np.array(df_train["x"]).reshape(-1,1), df_train["y_diff"])
y_diff_pred = reg.predict(np.array(df_test["x"]).reshape(-1,1))

# Add difference
y_pred = []
for i in range(0,len(df_test["x"])):
    if i == 0:
        y_pred.append(df_train["y"].iloc[-1] + y_diff_pred[i])
    else:
        y_pred.append(y_pred[i-1]+y_diff_pred[i])

print(y_pred)

# Show graph
plt.plot(df_train["x"], df_train["y"], label="y=0.5x(train)")
plt.plot(df_test["x"], df_test["y"], label="y=0.5x(test)")
plt.plot(df_test["x"], y_pred, label="y=0.5x(pred)")
plt.legend()
plt.show()

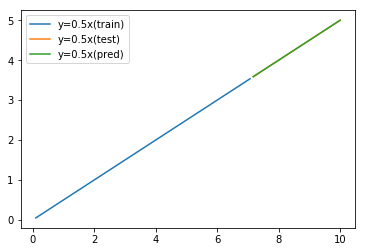
差分値を学習させたRandomForestの予測結果