

データの分析や処理に便利なBigQuery(BQ)。
大規模データの処理に優れており、テーブルに保存した大きなデータでも短時間で集計することができる。
BQの機能のひとつに、配列(array)があるが、配列をベクトルとして捉えた場合、ベクトル同士の類似度を計算したくなる。
ではどのようにコサイン類似度を計算すればいいのか。
そこで今回はBigQueryで配列(array)のコサイン類似度を計算する方法について紹介する。
この記事を書いている人

記事を読むメリット
BigQueryで配列(array)のコサイン類似度を計算する方法がわかり、ベクトルの類似度計算で困ることがなくなる。
コサイン類似度とは

コサイン類似度は2つのベクトルがどのくらい似ているかの指標。
コサイン cos は三角関数で、角度が0度なら1、90度で0、180度で-1になる関数である。
であれば逆にコサインの値がわかれば角度がわかるということ。
そして2本のベクトルの角度が0に近いということは、ベクトル同士が似ていると言えるので類似度として用いられる。
コサイン類似度とは、ベクトル空間モデルにおいて、文書同士を比較する際に用いられる類似度計算手法。
コサイン類似度は、そのまま、ベクトル同士の成す角度の近さを表現するため、三角関数の普通のコサインの通り、1に近ければ類似しており、0に近ければ似ていないことになる。参考:コサイン類似度
計算式としては以下の式で計算できる。
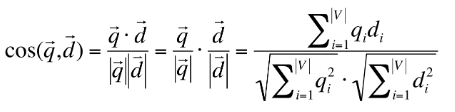 |
|---|

データ準備

では実際に計算してみるが、
まずはデータを準備する。
配列データを作るために前回配列データを作ったときのテーブルを再利用する。
あわせて読みたい
SQLに CREATE TABLE を追加してテーブルを作る。
SQL
CREATE TABLE test.array_sample2 AS SELECT key, ARRAY_AGG(val) as val_array FROM test.array_sample GROUP BY key
結果
| Row | key | val_array |
| 1 | a | 1 |
| 2 | ||
| 3 | ||
| 2 | b | 2 |
| 4 | ||
| 5 | ||
| 3 | c | 3 |
| 2 | ||
| -1 |
BigQueryで配列(array)のコサイン類似度を計算する方法

BigQueryで配列(array)のコサイン類似度を計算するには配列の要素同士の積を求める必要がある。
SQLは以下の通り。
SQL
SELECT
t1.key AS key1,
t2.key AS key2,
(
SELECT
SUM(value1 * value2)/ SQRT(SUM(value1 * value1))/ SQRT(SUM(value2 * value2))
FROM
UNNEST(t1.val_array) AS value1
WITH
OFFSET
pos1
JOIN
UNNEST(t2.val_array) AS value2
WITH
OFFSET
pos2
ON
pos1 = pos2 ) AS cosine_similarity
FROM
test.array_sample2 AS t1,
test.array_sample2 AS t2
ORDER BY
key1,
key2,
cosine_similarity
UNNEST(array) でarrayを1つ1つの要素にバラして WITH OFFSET pos でバラした要素に番号を振っている。
そしてposを結合のキーとして使うことで同じ番号の要素同士で掛け算できるようにしている。
そして結果は以下のようになる。
結果
| Row | key1 | key2 | cosine_similarity |
|---|---|---|---|
| 1 | a | a | 1 |
| 2 | a | b | 0.9960238411 |
| 3 | a | c | 0.2857142857 |
| 4 | b | a | 0.9960238411 |
| 5 | b | b | 1 |
| 6 | b | c | 0.3585685828 |
| 7 | c | a | 0.2857142857 |
| 8 | c | b | 0.3585685828 |
| 9 | c | c | 1 |
aとbはベクトルの方向が似ているのでコサイン類似度は高い値が出ているが、cは違う方向を向いているので類似度は低めとなっている。
まとめ

今回はBigQueryで配列(array)のコサイン類似度を計算する方法について解説した。
BigQueryで配列(array)のコサイン類似度を計算する方法は以下の通り。
ココがポイント

UNNEST(array)の使い方がちょっと難しいポイントですね他にもBigQueryに関する記事もあるので、興味があれば見てみて欲しい。




